Обработка результатов научных исследований

Страница 2

где: - максимальное и минимальное значение измерительной величины или погрешности.

Если вместо эмпирических частот y

1 …

yn

принять их вероятности

р1 … р

n

,

то это даст важную характеристику распределения – математическое ожидание:

Для непрерывных случайных величин математическое ожидание определяется интегралом:

т.е. оно равно действительному значению хд

наблюдаемых событий. Таким образом, если систематические погрешности измерений полностью исключены, то истинное значение измеряемой величины равно математическому ожиданию, а соответствующая ему абсцисса называется центром распределения. Площадь, расположенная под кривой распределения (рис.1), соответствующая единице, т.к. кривая охватывает все результаты измерений. Для одной и той же площади можно построить большое количество кривых распределения, т.е. они могут иметь различное рассеяние. Мерой рассеяния (точности измерений) является дисперсия или среднеквадратичное отклонение. Таким образом, дисперсия характеризует рассеивание случайной величины по отношению к математическому ожиданию и вычисляется по формуле:

Важной характеристикой теоретической кривой распределения является среднеквадратичное отклонение:

Коэффициент вариации

применяется для сравнения интенсивности рассеяния в различных совокупностях, определяется в относительных единицах (

k

в

<

1).

Основной задачей статистики является подбор теоретических кривых по имеющемуся эмпирическому закону распределения. Пусть в результате n измерений случайной величины получен ряд ее значений х1, х2, х3, …., х

n

. При первичной обработке таких рядов их вначале группируют в интервалы и устанавливают для каждого из них частоты

и . По значениям х

i

и строят ступенчатую гистограмму частот и вычисляют характеристики эмпирической кривой распределения. Основными характеристиками эмпирического распределения являются:

среднеарифметическое значение:

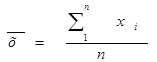
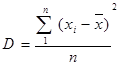
дисперсия:

Значения этих величин соответствуют величинам и теоретического распределения.

Уравнение 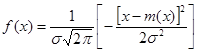соответствует функции нормального распределения при m(x)0 (рис. 2, а). Если совместить ось ординат с точкой m, т.е. m(x)=0 (рис.2,б), и принять , то знаки нормального распределения описываются зависимостью:

Для оценки рассеяния обычно пользуются величиной . Чем меньше , тем меньше рассеяние, т.е. большинство наблюдений мало отличается друг от друга (рис.3). С увеличением рассеяние возрастает, вероятность появления больших погрешностей увеличивается, а максимум кривой распределения (ордината), равная уменьшается. Поэтому величину при или называют мерой точности.

Конструирование и расчет сопряжения вспомогательной балки с главной
Сопряжение вспомогательной балки с главной производится через рёбра жёсткости. Опорная реакция вспомогательной балки равна: Принимаем болты нормальной точности, класс по прочности – 6,6, диаметром 20 мм. Расчетное сопротивление срезу болтов для принятого класса прочности Rbs = 230 Мпа. Расчетные усилия ...

Определение режима работы нс-ii
Выбор режима работы насосной станции второго подъема (НС-II) определяется графиком водопотребления (рис. 1.). В те часы, когда подача НС-II больше водопотребления поселка, избыток воды поступает в бак водонапорной башни (ВБ), а в часы, когда подача НС-II меньше водопотребления поселка, недостаток воды посту ...

Автобетоносмеситель 69360а (абс-6dа) (шасси камаз-53229 6х4)
Автобетоносмеситель предназначен для транспортирования отдозированных сухих компонентов бетонной смеси, перемешивания ее в пути следования и доставки готовой бетонной смеси на строительный объект. Автобетоносмеситель представляет собой реверсивный бетоносмеситель, установленный на надежном и экономичном ша ...