Обработка результатов научных исследований

Страница 4

.

Кроме приведенных выше применяют и другие виды распределений. В исследованиях часто возникает необходимость выявления факторов или их комбинаций, существенно влияющих на исследуемый процесс, так как при измерении какой-либо величины результаты обычно зависят от многих факторов. Практика показывает, что основными факторами, как правило, являются техническое состояние прибора и внимание оператора. Для установления основных факторов и их влияния на исследуемый процесс используется дисперсионный одно- и многофакторный анализ. Суть однофакторного дисперсионного анализа рассмотрим на примере. Пусть необходимо проверить степень точности группы m

приборов и установить, являются ли их систематические ошибки одинаковыми, т.е. изучить влияние одного фактора – прибора на погрешность измерения. Каждым прибором выполнено n

измерений одного и того же объекта, а всего nm

измерений. Отдельное измерение х

ij

, где i

– номер прибора, имеющий значение от 1 до m

;

j

- номер выполненного на этом приборе измерения, изменяющийся от 1 до n

.

Дисперсионный анализ допускает, что отклонения подчиняются нормальному закону распределения, в соответствии с которым вычисляют для каждой серии измерений среднеарифметическое значение и среднюю из показаний первого прибора и т.д. для каждого из ni

измерений и

mi

приборов.

В результате расчетов устанавливают величину Q1, называемую суммой квадратов отклонений между измерениями серий:

Она показывает степень расхождения в систематических погрешностях всех

m

приборов, т.е. характеризует рассеивание исследуемого фактора между приборами.

Здесь

-

среднеарифметическое для n измерений;

- среднеарифметическое для всех серий измерений, т.е. общее среднее значение.

Определяется также величина Q2

где х

ij

- отдельное

i

-е

измерение на

j

-ом

приборе.

Величину Q2 называют суммой квадратов отклонений внутри серии. Она характеризует остаточное рассеивание случайных погрешностей одного прибора.

При таком анализе допускается, что центры нормальных распределений случайных величин равны, в связи с чем все mn

измерения можно рассматривать как выборку из одной и той же нормальной совокупности. Чтобы убедиться в возможности такого допущения, вычисляют критерий:

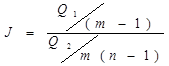
Числитель и знаменатель представляют собой дисперсию для m

и mn

наблюдений. В зависимости от значений k

1

=

m

-1

и k

2

=

m

(

n

-1)

числа степеней свободы и вероятности рсоставлены табличные значения J

т

.

Если J

≤

J

т

то считается, что в данном примере все приборы имеют одинаковые систематические ошибки.

Дисперсионный анализ является многофакторным, если он имеет два фактора и более. Суть его принципиально не отличается от однофакторного, но существенно увеличивается количество расчетов.

Методы теории вероятностей и математической статистики часто применяют в теории надежности, широко используемой в различных отраслях науки и техники. Под надежностью понимают свойство изделия (объекта) выполнять заданные функции (сохранять установленные эксплутационные показатели) в течение требуемого периода времени. В теории надежности отказы рассматривают как случайные события. Для количественного описания отказов применяются математические модели – функции распределения вероятностей интервалов времени.

Стройгенплан. Исходные данные для проектирования
Стройгенплан - важнейший документ для проектирования производства работ. Стройгенплан представляет собой общий план строительной площадки объекта с нанесением на нем мест расположения: · строящегося здания; · монтажных кранов; · складов открытого и закрытого хранения стройматериалов, элементов, деталей; ...

Тектоника сводчатых конструкций
Стоечно-балочная конструкция из камня не давала возможности создать достаточно обширные пространства, чтобы вместить огромные массы людей. Проблема была решена путём использования клинчатых арочных конструкций, сводов и куполов. Арочно-сводчатые конструкции позволили по-новому использовать свойства материал ...

Грузовая работа
Грузовая работа R тыс.м3км/год, определяется по формуле: (1.8) где a, b, c, d, e - длины участков пути, км; - коэффициент развития трассы. Принимаем a = 0,71 км; b = 0,57 км; c = 0,84 км; d = 0,26 км; e = 1,9 км; = 1,15; R = 112(0,71+0,26+1,9) 1,15 + 135(0,57+0,26+1,9) 1,15 + 99(0,84+1,9) 1,15 = 1096 ...