Обработка результатов научных исследований

Страница 3

Таким образом, чем меньше , тем больше сходимость результатов измерений, а ряд измерений более точен, среднеквадратичное отклонение определяет закон распределения. Отклонения + и - соответствуют точкам перегиба кривой (заштрихованная площадь на рис. 3). В общем случае для предела

вероятность того, что событие х

i

попадает в данный предел, вычисляется по распределению Лапласа:

При анализе многих случайных дискретных процессов пользуются распределением Пуассона. Так, вероятность появления числа событий х=1,2,3,…в единицу времени определяется законом Пуассона (рис.4) и подсчитывается по формуле:

Где х

– число событий

за данный отрезок времени t

;

- плотность, т.е. среднее число событий за единицу времени;

- число событий за время t

, =

m

Распределение Пуассона относят к редким событиям, т.е. р(х)

– вероятность того, что событие в период какого-то испытания произойдет храз при очень большом числе измерений m

. Для закона Пуассона дисперсия равна математическому ожиданию числа наступления события за время t

, т.е.

Для исследования количественных характеристик некоторых процессов можно применять показательный закон распределения (рис. 5). Плотность вероятности показательного закона выражается зависимостью . Здесь плотность является величиной, обратной математическому ожиданию , кроме того .

В различных областях исследований широко применяется закон распределения Вейбулла (рис.6). , где n

, - параметры закона; х

– аргумент (чаще принимаемый как время).

Исследуя процессы, связанные с постепенным снижением параметров (ухудшением свойств материалов во времени, деградация конструкций, процессы старения, износовые отказы в машинах и др.), применяют закон - распределения (рис. 7). 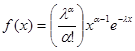; где - параметры. Если = 1, - функция превращается в показательный закон.

При исследовании многих процессов, связанных с установлением расчетных характеристик, материалов и т.п., используют закон распределения Пирсона (рис.8), чаще всего представляемый в виде:

где а

– максимальная ордината; d

,

b

– соответственно расстояния от максимальной ординаты до центра распределения С

и начала координат 0

Штатная ведомость цеха
Таблица 13 Штатная ведомость цеха Наименование профессии или вида работ Явочная численность, чел Длительность смены, ч Количество чел·ч I смена II смена III смена Всего В сутки В год Основные производственные рабочие Пост №1: рабочие 2 2 - 4 8 32 ...

Расчет комплекта автосамосвалов для транспортирования грунта
Коэффициент первоначального разрыхления грунта для суглинка тяжелого принимаем как среднее значение по табл. П1.11 Кпр=1,15, скорость автосамосвалов принимаем по таблице П1.10 как для грунтовых дорог. Расчет автотранспорта необходимо выполнить для вывозки основного объема грунта в котловане. Продолжительнос ...

Исходные данные
Исходными данными для выполнения курсовой работы являются: - инженерно-геологические условия района строительства , которые принимаются по результатам ранее выполненной курсовой работой по механике грунтов; - физико-механические характеристики грунтов основания , численные значения которых принимаются по ...